Research

Much of my research to date has involved using the special function theory of the Schottky-Klein prime function to solve complex variable problems in multiply connected domains, e.g. conformal mapping, Hele-Shaw flows and vortex dynamics. I have recently become interested in harmonic analysis and Riemann surface theory.

The Schottky-Klein prime function

The Schottky-Klein prime function is a special transcendental function which plays a central role in problems involving multiply connected domains; despite this, it has been scarcely used by pure and applied mathematicians since it was originally written down (independently by both Schottky and Klein towards the end of the 19th century). In fact, this function can be used to great advantage in many varied applications – with it often being used to solve the problem for any number of boundaries - as has been increasingly demonstrated over the past decade. It also has a particularly rich function theory.

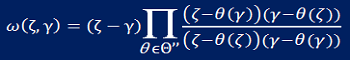
The need to compute this function effectively and accurately is therefore of paramount importance. With Darren Crowdy, Everett Kropf and Mohamed Nasser (here), a novel numerical method has been devised around which some new versatile software has been built to facilitate its computation in a straightforward way. At present, with Lesley Ward and Marie Snipes, the Schottky-Klein prime function is being used to compute various harmonic measure distribution functions in multiply connected domains arising in problems associated with Brownian motion.

Hele-Shaw flows

Hele-Shaw flows arise when two fluids of differing viscosities between close-to-touching parallel plates come together. Hele-Shaw flows were originally used to generate streamline patterns around various bodies for two-dimensional inviscid flows at the turn of the twentieth century; since then, they have been well-studied because they are an important paradigm of Laplacian growth processes. Bubbles and fingers are typical features in these flows.

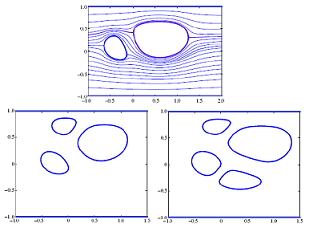
With Giovani Vasconcelos (here), all solutions for the conformal maps determining the shapes of assemblies of steadily translating bubbles in a Hele-Shaw channel have been found. This problem is an example of a free boundary problem (a problem where the boundary itself must be determined as part of the solution) in a multiply connected domain (a domain with more than one boundary). We appealed to special types of conformal mappings called Schwarz-Christoffel maps which can be written down as indefinite integrals of products of Schottky-Klein prime functions.

Many results for Hele-Shaw flows assume the absence of surface tension, including the Green & Vasconcelos solutions. More recently, with Scott McCue and Christopher Lustri, the effect of adding surface tension to the bubble boundaries has been analysed. Doing so gives rise to interesting problems called selection problems (here).

Vortex dynamics

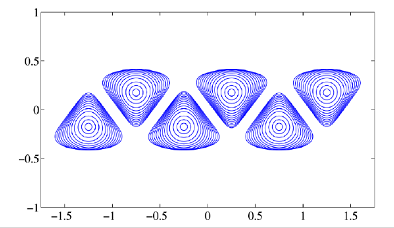
The classical model of a point vortex is insightful when devising basic mathematical models of fluid flows but is inherently flawed, not least because of their singular behaviour. Distributed vorticity or finite-area vortex models are more realistic, and the hollow vortex is one such example. A hollow vortex is a finite-area vacuum where the vorticity is concentrated on its boundary.

The hollow vortex model is a classical one, yet many solutions describing them have only been found relatively recently. They give rise to interesting types of free boundary problem. The so-called von Karman vortex street is ubiquitous in nature and often generated in the wake of bluff bodies. With Darren Crowdy (here), analytical solutions for the shapes of the hollow vortex boundaries in a von Karman street configuration were found. More recently, I found more analytical solutions describing the hollow vortex pair and a single row of hollow vortices in an infinite channel geometry (here).

Function theory on compact Riemann surfaces

Function theory on the sphere is well-understood and was largely motivated by the desire to study various phenomena on Earth. A common approach used to deal with such problems is the stereographic projection of the sphere onto the plane. A natural question is how to extend such investigations to other compact Riemann surfaces.

With Jonathan Marshall (here), the first closed-form expression for the Green’s function of the Laplace-Beltrami operator on a toroidal surface was found. Our technique relied upon the stereographic projection of the torus to a concentric annular plane, wherein we could use the function theory of Schottky-Klein prime function. Such a Green’s function can also be regarded as a streamfunction for an ideal vortex flow on the surface of the torus.

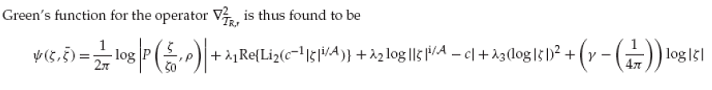
Numerical conformal mapping

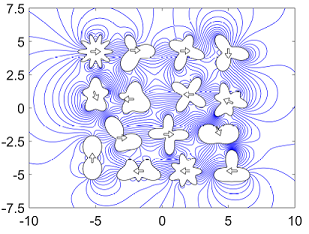
Recently, with Mohamed Nasser, the determination of the flow field generated by assemblies of fluid stirrers can be formulated as a Riemann-Hilbert problem defined over a multiply connected domain and may be readily solved numerically through a particular boundary integral equation having as its kernel function the so-called generalized Neumann kernel. For a large number of stirrers, the numerical scheme is very fast and produces accurate results.

With Darren Crowdy and Athanassios Fokas (here), the construction of special types of conformal mappings called polycircular arc mappings is presented. We show these conformal mappings are solutions of a third-order nonlinear oridinary differential equation involving various Schwarzian derivatives.